Keterangan
Input : Sebuah n x n matriks A, dan m x 1 vektor b, mewakili m persamaan linear dengan n variabel.
Masalah : Apa vektor x sehingga A \ cdot x = b.
Pemecahan sistem linear merupakan masalah penting ilmiah dan komersial. Ada kemungkinan ada alasan yang baik untuk membuat solver Anda sendiri, meskipun algoritma dasar (Gaussian elimination) adalah salah satu yang kita pelajari di sekolah tinggi. Hal ini berlaku jika Anda bekerja dengan sistem yang besar.
Gauss elimination didasarkan pada kenyataan bahwa solusi untuk sistem persamaan linear invarian pada skala (mengalikan kedua sisi dengan konstan, yaitu jika x = y, maka 2x = 2y) dan menambahkan persamaan (yaitu solusi untuk persamaan x = y dan w = z adalah sama dengan solusi untuk x = y dan x + w = y + z). sisik eliminasi Gauss dan menambahkan persamaan sehingga dapat menghilangkan setiap variabel dari semua kecuali satu persamaan, meninggalkan sistem dalam keadaan seperti itu bahwa solusi hanya dapat dibaca dari persamaan.
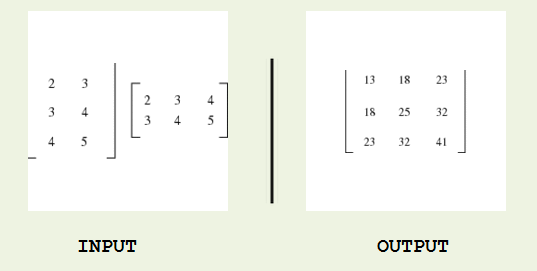
Matrix Multiplication(Perkalian matriks)
Operasi Dasar Matriks :
1. Penjumlahan dan Pengurangan Matriks
Elemen-elemen dalam suatu matriks yang dijumlahkan atau dikurangan yaitu elemen yang memilki posisi/letak yang sama barulah matrik bisa melakukan penjumlahan/pengurangan.
2. Perkalian Skalar
Untuk Melakukan perkalian matrik banyaknya kolom pada matrik pertama harus sama dengan banyaknya baris pada matrik ke 2 ,seletah itu barulah kita kalikan matrik pada baris pertama dengan matrik kolom pertama ,dan seterusnya .
Bilangan yang menunjukan banyaknya baris (m) dan banyaknya kolom (n) disebut ordo suatu matrik.
Matriks Identitas matriks yang anggota pada diagonal utamanya selalu 1 di sebut
Matriks Identitas .
maka matriks transposenya (At) adalah
Determinan Suatu Matriks
Untuk menentukan determinan dari suatu matriks dapat digunakan beberapa cara :
1. Misalnya terdapat matriks yang berordo 2×2 dalam menentukan determinan dari matrikas A yang biasa ditulis |A| adalah
2. Metode Sarrus
Misalnya terdapat maka untuk menentukan nilai determinan dari matriks A tersebut
Ubah matriks dalam bentuk seperti diatas selanjutnya perhitungannya dengan cara menambahkan elemen dari kiri atas kekanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) kemudian dikurangi dengan elemen dari kanan atas kekiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i)
3. Metode Ekspansi Baris dan Kolom
Jika diketahui maka untuk menentukan determian dari matriks P
Matriks Singular
Matriks Singular yaitu matriks yang nilai determinannya 0.
Invers Matriks
Misalnya diketahui maka invers dari matriks A
Sifat-sifat dari invers suatu matriks :
Persamaan Matriks
Tentukan X matriks dari persamaan:
Referensi
Matrik
Matrix Multiplication(Perkalian matriks)
Matrik adalah sekumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun
menurut baris dan kolom. Bilangan-bilangan yang terdapat pada suatu
matriks disebut dengan elemen atau disebut juga anggota dari suatu
matriks.
Matriks juga
seperti variabel biasa, sehingga matrik spun dapat dimanipulasi misalnya
dikalikan, dijumlah, dikurangkan, serta didekomposisikan. Menggunakan
representasi matriks, perhitungan dapat dilakukan dengan lebih
terstruktur.
Kegunaan Matrik
Matrik memiliki banyak manfaat yaitu untuk
menyelesaikan berbagai permasalahan matematika misalnya dalam menemukan
solusi masalah persamaan linear, transformasi linear yakni bentuk umum
dari fungsi linear contohnya rotasi dalam 3 dimensi.
Operasi Dasar Matriks :
1. Penjumlahan dan Pengurangan Matriks
Elemen-elemen dalam suatu matriks yang dijumlahkan atau dikurangan yaitu elemen yang memilki posisi/letak yang sama barulah matrik bisa melakukan penjumlahan/pengurangan.
2. Perkalian Skalar
Untuk Melakukan perkalian matrik banyaknya kolom pada matrik pertama harus sama dengan banyaknya baris pada matrik ke 2 ,seletah itu barulah kita kalikan matrik pada baris pertama dengan matrik kolom pertama ,dan seterusnya .
Bilangan yang menunjukan banyaknya baris (m) dan banyaknya kolom (n) disebut ordo suatu matrik.
Matriks Identitas matriks yang anggota pada diagonal utamanya selalu 1 di sebut
Matriks Identitas .
Matriks Transpose (At)
Matriks transpose merupakan matriks yang mengalami pertukaran elemen dari kolom menjadi baris atau sebaliknya. Contoh :maka matriks transposenya (At) adalah
Determinan Suatu Matriks
Untuk menentukan determinan dari suatu matriks dapat digunakan beberapa cara :
1. Misalnya terdapat matriks yang berordo 2×2 dalam menentukan determinan dari matrikas A yang biasa ditulis |A| adalah
2. Metode Sarrus
Misalnya terdapat maka untuk menentukan nilai determinan dari matriks A tersebut
Ubah matriks dalam bentuk seperti diatas selanjutnya perhitungannya dengan cara menambahkan elemen dari kiri atas kekanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) kemudian dikurangi dengan elemen dari kanan atas kekiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i)
3. Metode Ekspansi Baris dan Kolom
Jika diketahui maka untuk menentukan determian dari matriks P
Matriks Singular
Matriks Singular yaitu matriks yang nilai determinannya 0.
Invers Matriks
Misalnya diketahui maka invers dari matriks A
Sifat-sifat dari invers suatu matriks :
Persamaan Matriks
Tentukan X matriks dari persamaan:
- Jika diketahui matriks A.X=B
- Jika diketahui matriks X.A=B
Referensi
Matrik

No comments:
Post a Comment